1. 什么是正则化
正则化通过在损失函数中引入惩罚项来限制模型的复杂度,以防止模型过度拟合训练数据。惩罚项会在优化过程中对模型的参数进行调整,以平衡模型的拟合能力和泛化能力。
正则化的作用如下:
- 防止过拟合:正则化通过限制模型的复杂度,减少模型对训练数据的过度拟合,提高模型的泛化能力
- 特征选择:L1 正则化可以使得部分参数变为 0,从而实现特征选择,减少冗余特征的影响
- 改善模型稳定性:正则化可以降低模型对数据中噪声的敏感性,提高模型的稳定性
常见正则化方法有 L1 正则化、L2 正则化和 Dropout。
2. L1 正则化
对于待正则的网络参数 $w$,L1 正则化: $$ L_1=\lambda||w||_1=\lambda\sum_i|w_i| $$ 其中,$\lambda$ 用来控制正则程度的大小。L1 不仅可以约束参数量,还可以是参数更稀疏,即部分参数为零(部分特征被去除),实现了特征选择。
L1 正则化的优点和应用如下:
- 特征选择:L1 正则化倾向于生成稀疏的参数,即将一部分参数变为 0,减少冗余特征,实现特征选择
- 模型解释性:L1 正则化的特征选择能够确定对预测结果贡献较大的特征,一定程度上解释模型的结果
- 防止过拟合:限制模型的复杂度,防止模型过度拟合训练数据
- 稀疏性:L1 正则化可以产生稀疏的参数,使得模型的计算效率更高,减少存储空间
3. L2 正则化
对于待正则的网络参数 $w$,L2 正则化: $$ L_2=\lambda||w||_2=\lambda\sum_{i}{|w_i|^2} $$ L2 正则化会使部分特征趋近于 0,达到正则化的效果。
L2 正则化的优点和应用包括:
- 参数稳定性:L2 正则化可以使模型参数更稳定,减少参数的震荡,使模型对噪声和细节不敏感,提高模型的泛化能力。
- 防止过拟合:L2 正则化限制了模型参数的大小,使得模型更加平滑。
- 权重衰减:L2 正则化可以促使模型参数向较小的值靠拢,实现权重衰减,减少复杂模型对训练数据的过度拟合。
L1 正则化和 L2 正则化可以被联合使用,这种方法被称为 Elastic Net 正则化,它综合了两者的优势。可以同时实现特征选择和参数大小的控制。
4. L1 正则化使得模型参数具有稀疏性的原理是什么
4.1 解空间形状
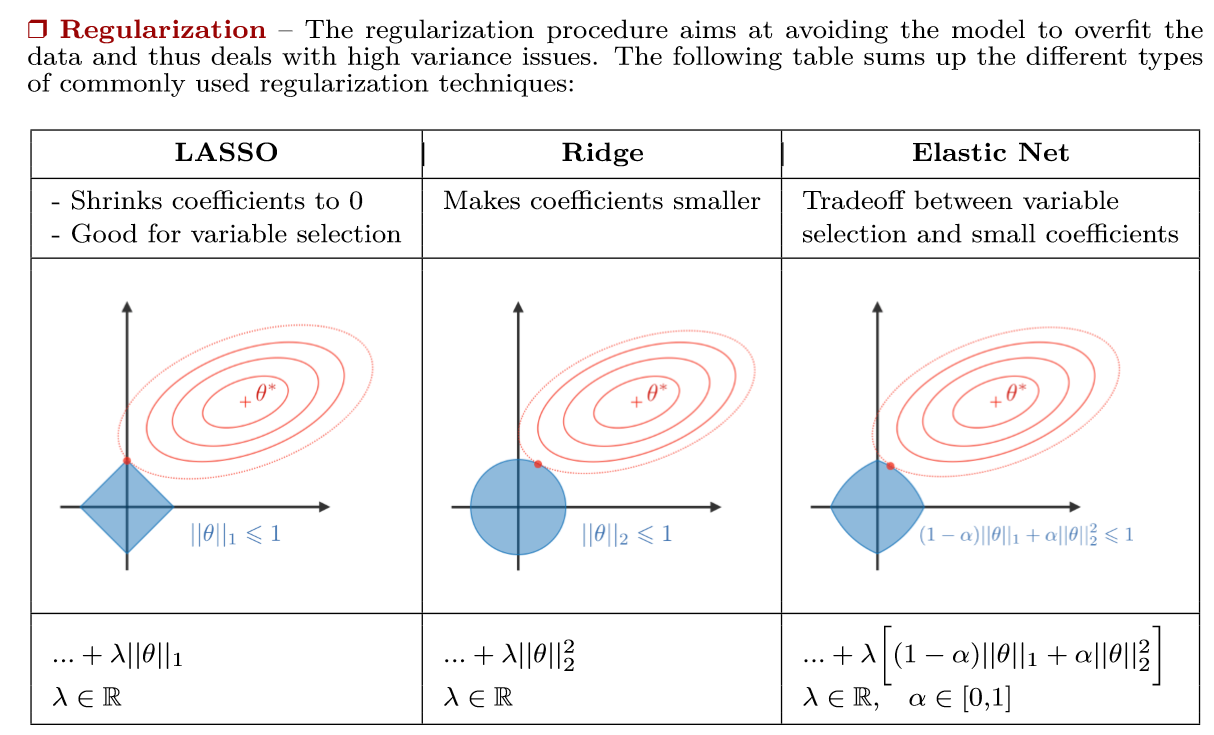
如下图,在二维情况下,黄色部分为 L2 和 L1 正则约束后的解空间(相当于约束 $w$ 的范数不能超过常数 m),蓝色等高线是凸优化问题中目标函数的等高线。最小化损失函数就是求蓝圈+黄圈的和的最小值,显然 L1 正则的解空间更容易在夹角处与等高线碰撞出稀疏解。

4.2 函数叠加
如下图,棕线是原始目标函数 $L(w)$ 曲线图,显然最小值在蓝点处,对应的 $w^*$ 值非 0。

考虑加上 L2 正则化项,目标函数变为黄线 $L(w)+Cw^2$,最小值在黄点处,对应 $w^*$ 绝对值减小了,仍然非 0。
考虑加上 L1 正则化项,目标函数变为绿线 $L(w)+C|w|$,最小值在红点处,对应 $w^*$ 为 0,产生了稀疏性。
由于加入 L1 正则化项,对目标函数求导,在原点左侧为 -C,右侧为 C,只要原目标函数导数绝对值小于 C,那么带正则项的目标函数在原点左侧递减,右侧递增,即最小值点在原点处。
相反 L2 正则化项在原点处的导数为 0,只要原始目标函数导数值在原点不为 0,那么最小值点就不会在原点。所以 L2 正则项只有减小 w 绝对值的作用。
4.3 贝叶斯先验
L2 正则化相当于引入了高斯先验,L1 正则化相当于对模型参数引入了拉普拉斯先验,使参数为 0 的可能性更大。
下图为高斯分布曲线图,可见高斯分布在极值处是平滑的,即取不同值的可能性是接近的,因此 L2 正则化只会让 $w$ 更接近 0 点,但不会等于 0。

下图为拉普拉斯分布曲线图,可见拉普拉斯分布在极值点是一个尖峰,所以 $w$ 的取值为 0 的概率更大。

5. Dropout 的作用和原理
Dropout 在前向传播时,以一定的概率使部分神经元停止工作,增强模型泛化性。

前向传播:以概率 p 丢弃 K 维输入向量 $[x_1,x_2,\dots,x_k]$ 的某些值,有 $$ x’ = dropout(x) $$ 其过程相当于生成一个随机的 K 维 mask,下式中 @ 表示点乘: $$ r = rand(K) = [r_1,r_2,\dots,r_k],0\leq r_i\leq 1\\ mask=\begin{cases}0,r_i<p\\1,r_i\geq p\end{cases}\\ x’=dropoout(x)=x@mask $$ 这样的 dropout,在训练中会使 x’ 的期望改变: $$ E(X’)=p*0+(1-p)*x=(1-p)x $$ 在测试时,dropout 不工作,此时 x’ 的期望为 x,使得训练和测试时的期望不一致,因此在训练时,可以将 dropout 后的结果除以 1-p,此时 mask 为: $$ mask=\begin{cases}0,r_i<p\\\frac{1}{1-p},r_i\geq p\end{cases} $$ 反向传播: $$ x=[x_1,x_2,\dots,x_k]\ x’=dropout(x)=x@mask\ y=forward(x’) $$ 则有 $$ \frac{\partial y}{\partial x}=\frac{\partial y}{\partial x’}\cdot\frac{\partial x’}{\partial x} $$
其中 $$ \frac{\partial x’}{\partial x}= \begin{cases} 0,r_i<p\\ \frac{1}{1-p},r_i\geq p \end{cases} $$
6. L1 正则化的缺点
- 非光滑性:L1 正则化的正则化项是参数的绝对值之和,这导致目标函数在参数为零时不可导。在参数为零附近,梯度不连续,可能导致优化过程出现问题。
- 特征选择过于严格:当特征之间存在高度相关性(多重共线性)时,L1 正则化倾向于选择其中一个特征,而忽略其他相关特征,可能会丢失有用信息。相比之下,L2 正则化对相关特征的惩罚更均衡,可以保留更多相关特征的权重。
- 不适用于高维问题:虽然 L1 正则化在稀疏数据下表现出色,但对于高维稀疏数据,特征的选择过程可能不够稳定,可能会因微小的数据变动而导致不同的特征被选择。
7. BatchNorm 的原理和作用
BN 对每个批次的输入进行归一化,将输入的均值和方差调整到一个稳定的范围内,用于解决深度网络梯度消失和梯度爆炸的问题,可以起到一定的正则化作用。
首先计算 mini-batch 的均值 $\mu$ 和方差 $\sigma^2$,然后进行规范化得到: $$ x_i^*=\frac{x_i-\mu}{\sqrt{\sigma^2+\epsilon}} $$
最后进行尺度变换和偏移得到:
$$ y_i=\gamma\cdot x^*_i+\beta $$
BN 是一个可学习、有参数($\gamma,\beta$)的网络层。
8. BN 的训练和推理有什么不同
BN 在训练时会更新
BN 训练时记录每个 batch 的均值和方差,测试时用全部训练数据的均值(期望)和方差(无偏估计)。 $$ E[x]\leftarrow E_\beta[\mu_\beta]\\ Var[x]\leftarrow\frac{m}{m-1}E_\beta[\sigma_\beta^2] $$ 推理使用训练阶段累积的统计量(均值和方差的移动平均值)来进行标准化。将训练时的均值和方差的平均值代入如下公式即可: $$ y=\frac{\gamma}{\sqrt{Var[x]+\epsilon}}\cdot x+(\beta-\frac{\gamma\cdot E[x]}{\sqrt{Var[x]+\epsilon}}) $$ 有$\frac{\gamma}{\sqrt{Var[x]+\epsilon}}$ 和 $(\beta-\frac{\gamma\cdot E[x]}{\sqrt{Var[x]+\epsilon}})$ 两项固定值,可以加速计算。
即使在推理时输入是 mini-batch,也应该使用训练时的移动平均值和方差,这样是为了保证模型在训练和推理时行为的一致性。
9. BN 的可学习参数作用
BN 有 $\gamma,\beta$ 两个可学习的平移参数和缩放参数,具有以下作用:
- 保留网络各层在训练过程中的学习成果。若没有这两个参数,BN 退化为普通的标准化,不能有效学习。添加参数后可以保留每个神经元学习的成果;
- 保证激活单元的非线性表达能力。添加参数后,BN 的数据可以进入到激活函数的非线性区域;
- 使 BN 模块具有自我关闭功能。若 $\gamma,\beta$ 分别取数据的均值和标准差,则可以回复初始的输入值,即关闭 BN 模块。
10. BN 和 LN 的区别
BN 是在每个批次中对每个特征的维度进行归一化。LN 是在每一层中对每个样本的所有特征维度进行归一化。
BN 适用于批次训练的情况,LN 更适用于变长序列数据的处理。
如以下两图,直观地展示了 BN、LN、IN 和 GN 的区别。


11. 将 BN 用于推荐系统时的注意事项
- 数据稀疏性:推荐系统的输入往往非常稀疏,直接使用 BN 可能导致不稳定的统计量,BN 通常在嵌入层之后的稠密表征或者深层网络中表现得更好;
- 动态范围的特征:在推荐系统中,某些特征的范围可能动态变化,可能需要频繁地更新 BN 的统计数据或考虑使用其他归一化技巧;
- 序列化的数据:推荐系统中经常处理序列化的数据,例如用户的行为序列,BN 不适用。